Diese Seite funktioniert nur mit Javascript.
Indifferenzkurven2.2.4 Die Grenzrate der SubstitutionDas Haushaltsoptimum
ndifferenzkurven verraten durch ihre Gestalt etwas über die Präferenzen des Haushalts. Kein Wunder, denn sie bilden die Präferenzen ja ab. Die Information, die man aus ihnen ablesen kann, geht aber noch etwas weiter, denn man kann ansatzweise erkennen, wie der Haushalt die Güter verwendet. Dazu betrachten wir die folgenden Abbildungen.
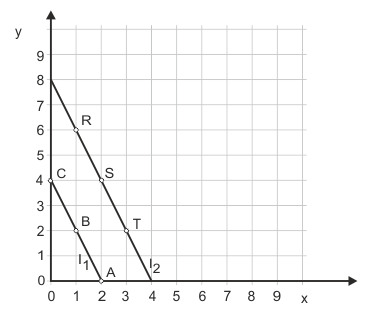
Beide Indifferenzkurven lassen erkennen, dass der Haushalt indifferent bleibt, wenn aus einem Güterbündel 2 Y entfernt werden und dafür 1 X hinzugefügt wird. Dabei spielt es keine Rolle, ob der Haushalt anfangs über viel oder wenig Y verfügt. Offenbar lassen sich in den Augen des Haushalts 2 Y perfekt durch 1 X ersetzen.
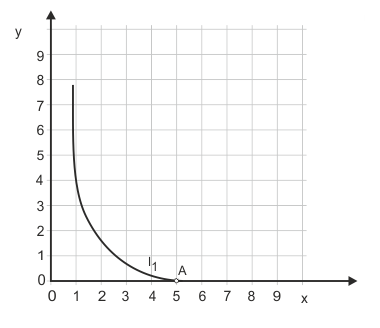
In Abbildung 2 endet die Indifferenzkurve in A (kein Y, 5 X). Der Haushalt ist bereit, vollkommen auf das Gut Y zu verzichten. Y lässt sich also in seinen Augen gänzlich durch X ersetzen. Daher spricht man bei Y von einem vollkommen substituierbaren Gut. Erreichen die Indifferenzkurven die Achsen nicht, heißen die Güter teilweise substituierbar. Eine Ausnahme bildet der Grenzfall in Abbildung 3.
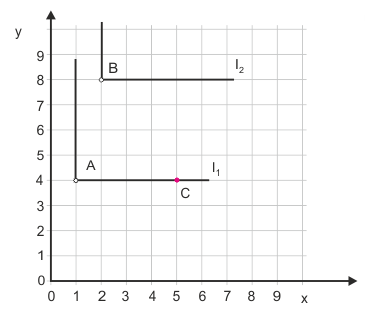
Abbildung 3 zeigt einen Grenzfall, der der Nichtsättigungsannahme widerspricht, nach der die Indifferenzkurven fallenden Verlauf zeigen müssen. (Um die Annahme aufrecht halten zu können, müsste man beide Teilbereiche der Kurve leicht neigen.) Wenn der Haushalt nur von einem Gut mehr erhält, erreicht er keinen höheren Nutzenindex. Das ist vorstellbar, wenn die Güter in einem festen Verwendungszusammenhang stehen, also strenge Komplementärgüter sind. Was nutzt das 5., 6. oder 7. Rad an einem vierrädrigen Handwagen? Was nutzt der zweite rechte Schuh?
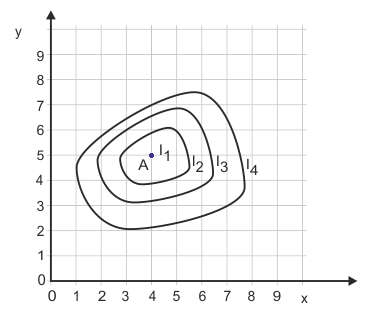
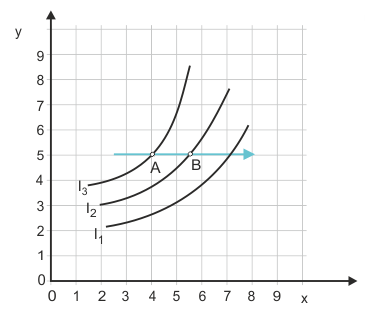
Abbildung 4 zeigt einen Fall, der eklatant gegen die Nichtsättigungsannahme verstößt. Der höchste Nutzenindexwert soll bei I1 erzielt werden, der kleinste auf I4. I1 zeigt damit das optimale Güterbündel für den Haushalt an.
Auch Abbildung 5 zeigt Indifferenzkurven, die auf den ersten Blick gegen die Nichtsättigungsannahme verstoßen. Wenn es sich bei X aber nicht um ein Gut, sondern um ein "Schlecht" ( Ungut) handelt, kann dieser Indifferenzkurvenverlauf Sinn machen. Beispiele für solche Ungüter wären Müll oder Arbeit. Von beidem ist weniger mehr, daher kommt der Haushalt auf niedrigere Nutzenindexwerte, wenn er sich in Pfeilrichtung von A nach B bewegt. Wenn X für Arbeitszeit und Y für Konsumgüter steht, dann zeigt A im Vergleich zu B bei gleichem Konsumniveau eine kürzere Arbeitszeit und somit eine bevorzugte Situation für den Haushalt.
Man kann durch Umdefinieren in aller Regel aus Ungütern Güter machen: Müll - Müllvermeidung, Arbeitszeit - Freizeit. Das Ungut erhielte ein negatives Vorzeichen und würde zum Gut. Im Diagramm käme das einer Spiegelung an der Achse für das Gut Y gleich, so dass die Indifferenzkurven wieder fallenden Verlauf zeigen würden.
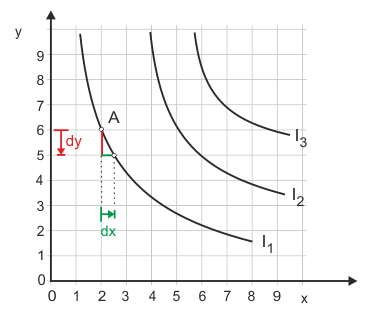
Im Regelfall geht man von einer "typischen" Indifferenzkurvenschar. Die Güter sind begrenzt substituierbar. In Abbildung 6 ist dargestellt, welche Menge (${\rm{d}}x$) des Gutes X notwendig ist, den Nutzen des Haushalts konstant zu halten, wenn er eine Einheit (${\rm{d}}y$) des Gutes Y aufgibt. Das Verhältnis dieser beiden Mengen heißt Grenzrate der Substitution (${{{\rm{d}}x} \over {{\rm{d}}y}}$). Der Begriff Substitutionsrate wäre sicher sprechender, brächte er doch unmittelbar zum Ausdruck, in welcher Rate die Güter gegeneinander substituiert werden können. Der Wortteil "Grenz-" soll darauf hinweisen, dass nur kleine Änderungen in der Umgebung des jeweiligen Ausgangspunktes betrachtet werden. Wenn man sich von diesem Punkt entfernt, ändert sich die Rate (es gibt Ausnahmen, z. B. im Fall von Abb. 1).
Die Grenzrate der Substitution kann in zwei Richtungen betrachtet werden. 1. Wieviel von Gut X ist erforderlich, um eine Einheit von Gut Y zu ersetzen? Oder 2.: Wieviel von Gut Y ist erforderlich, um eine Einheit von Gut X zu ersetzen? Den ersten Fall sehen Sie in Abbildung 6 illustriert. Konvention ist allerdings, die Grenzrate der Substitution mit dem (absoluten) Wert der Steigung der Indifferenzkurve gleichzusetzen. Das entspricht dem 2. Fall (${\rm{GR}}{{\rm{S}}_{x,y}} = {{{\rm{d}}y} \over {{\rm{d}}x}}$; lies: Grenzrate der Substitution von Gut X durch Gut Y).Die Grenzrate der Substitution zeigt das Tauschverhältnis zweier Güter bei Indifferenz des Haushalts. Für die meisten Haushalte dürfte die Grenzrate der Substitution zwischen 100- und 10-Euro-Scheinen bei 10 liegen. Dabei geht man in der Regel recht nachlässig mit dem Begriff um. Auch den Kehrwert 1/10 hätte man akzeptiert, da - wenn man nicht auf die mathematische Formulierung zurückgreift - aus dem Gesagten oft nicht so recht klar wird, ob das Gut X durch das Gut Y oder das Gut Y durch das Gut X substituiert wird. Der Zusammenhang macht dies aber meist deutlich. Es dürfte klar sein, dass der Nutzen des Haushalts nicht konstant bleibt, wenn er für einen 10-Euro-Schein zehn 100-Euro-Scheine aufgibt.
Um diese Aussage einsehen zu können, betrachten wir ein Kind, das bei Indifferenz fünf Stück Schokolade gegen drei Murmeln zu tauschen bereit ist. "Bei Indifferenz" bedeutet einen konstanten Nutzenindexwert: Der Wert der Nutzenfunktion ist vor und nach dem Tausch gleich, d. h. seine Veränderung ist null (mit dem Symbol ${\rm{d}}$ für Änderung: ${\rm{d}}U = 0$).
Erinnern wir uns an den Grenznutzenbegriff: Es ist der Anstieg des Nutzens durch eine weitere Einheit eines Gutes. Den Grenznutzen einer Murmel nennen wir $\rm{GN}_M$. Den Grenznutzen eines Schokostücks $\rm{GN}_S$. Da das Kind bei Indifferenz fünf Schokostücke aufzugeben bereit ist, wenn es dafür drei Murmeln erhält, gilt für die Nutzenindexwertänderung
$${\rm{d}}U = - 5 \cdot {\rm{G}}{{\rm{N}}_M} + 3 \cdot {\rm{G}}{{\rm{N}}_S} \tag{1}$$also
$${5 \over 3} = {{{\rm{G}}{{\rm{N}}_M}} \over {{\rm{G}}{{\rm{N}}_S}}} \tag{2}$$Auf der linken Gleichungsseite steht das Tauschverhältnis von Schokostückchen und Murmeln - die (absolute) Grenzrate der Substitution - und auf der rechten das umgekehrte Verhältnis ihrer Grenznutzen.
Zu dieser Erkenntnis wäre man natürlich schneller gelangt, wenn man das totale Differenzial der Nutzenfunktion gleich null setzt: $$U = U\left( {x,y} \right) \tag{3}$$ $${\rm{d}}U = {{\partial U} \over {\partial x}} \cdot {\rm{d}}x{\rm{ + }}{{\partial U} \over {\partial y}} \cdot {\rm{d}}y = 0 \tag{4}$$ $${{{{\partial U} \over {\partial x}}} \over {{{\partial U} \over {\partial y}}}} = - {{{\rm{d}}y} \over {{\rm{d}}x}} \tag{5}$$
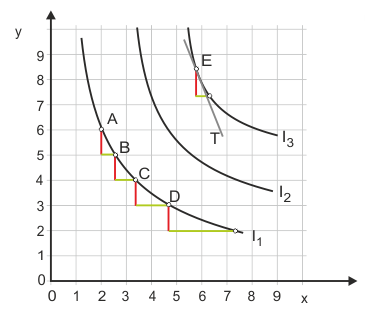
Auf der linken Seite in Gleichung (5) steht das Verhältnis der Grenznutzen, auf der rechten das (negative umgekehrte) Austauschverhältnis der Güter, das der Steigung der Indifferenzkurve entspricht.* Dies wird in Abbildung 7 beim Punkt E angedeutet, wo man durch die Tangente T den Zusammenhang zwischen der Steigung der Indifferenzkurve und dem Tauschverhältnis der Güter bei Indifferenz erkennen kann.
Gleichung (5) kann man auch entnehmen, dass die Steigung der Indifferenzkurve negativ sein muss, wenn beide Grenznutzen positiv sind. In Abbildung 5 haben wir ein Gegenbeispiel gesehen. Hier war der Grenznutzen des (Un)Gutes X negativ.
Nun könnte man auf die Idee kommen, die Überlegungen bauten auf der Annahme kardinal messbaren Nutzens auf, da in Gleichung (5) der Grenznutzen vorkommt. Die Aussage, dass die Grenzrate der Substitution gleich dem umgekehrten negativen Verhältnis der Grenznutzen ist, kommt jedoch ohne diese Annahme aus. Durch die Verhältnisbildung kürzt sich die Dimension des Nutzens heraus. Auf beiden Seiten (natürlich auf beiden ...) in Gleichung (5) ist die Dimension Mengeneinheiten des Gutes Y durch Mengeneinheiten des Gutes X. Das macht auch noch einmal deutlich, dass die Nutzenfunktion (streng positiv monoton) transformiert werden kann und trotzdem weiterhin dieselbe Präferenzordnung repräsentiert.* Würde man alle Nutzenindexwerte z.B. verdoppeln, dann würde sich Gleichung (5) trotzdem nicht verändern, denn man erhielte für die beiden Grenznutzen über und unter dem Bruchstrich jeweils auch den doppelten Wert. Auch die Käsebrötchen-Bier-Indifferenzkurven, die wir in Abb. 3 im vorigen Abschnitt betrachtet haben, würden für die Nutzenfunktion $U = 2 \cdot KB$ genau so aussehen wie für die Nutzenfunktion $U = KB$. Nur die Nutzenindexwerte an den beiden eingezeichneten Indifferenzkurven müssten von 8 und 20 auf 16 und 40 verdoppelt werden.
Abbildung 7 zeigt für den typischen Indifferenzkurvenverlauf, wie sich die Grenzrate der Substitution verändert. Je weniger vom Gut Y vorhanden ist, desto mehr Einheiten von X erwartet der Haushalt im Tausch für ein Y. Mit anderen Worten: Je knapper ein Gut wird, desto wertvoller wird es für den Haushalt gemessen in Einheiten des anderen Gutes. Diesen Effekt kann man im täglichen Leben sehr schön beobachten, wenn sich ein Süßigkeitenvorrat langsam dem Ende zuneigt. Solange die Bonbontüte noch voll oder die Tafel Schokolade kaum angebrochen ist, reicht das Zauberwort mit zwei t, um etwas abzubekommen. Beim vorletzten oder letzten Stück traut man sich aber kaum noch zu fragen. Ein ähnliches Verhalten ist bei Rauchern zu beobachten, die sich gegenseitig bei vollen Schachteln großzügig Zigaretten anbieten, aber plötzlich ganz knauserig werden, wenn sich ihr Bestand dem Ende zuneigt.
Da man dieses Phänomen recht durchgängig bei vielen Gütern zu beobachten meint, hat man es in den Status eines Gesetzes erhoben: das Gesetz von der abnehmenden Grenzrate der Substitution (s. Abb. 7). Für die in Abbildung 1 dargestellten Präferenzen gilt es allerdings nicht. Lineare Indifferenzkurven zeigen eine konstante Grenzrate der Substitution (denn ihre Steigung ist ja konstant).
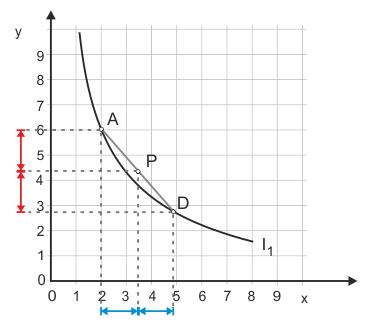
Wenn die Grenzrate der Substitution stetig abnimmt, dann müssen die Indifferenzkurven einen konvexen Verlauf zeigen. Wenn sie das tun, dann kann man zwischen zwei beliebigen Punkten auf einer Indifferenzkurve wie A und D in Abbildung 8 eine Verbindungslinie ziehen, die immer oberhalb der Indifferenzkurve liegt. Genau auf halber Strecke der Verbindungslinie findet sich das Güterbündel P, das von beiden Gütern jeweils die durchschnittlichen Mengen der Güterbündel der Endpunkte A und D enthält (die beiden blauen und roten Pfeile sind jeweils gleich lang).* Das "ausgewogene" Güterbündel P liegt auf einer höheren Indifferenzkurve. Also bevorzugt der Haushalt ausgewogene zusammengesetzte Güterbündel gegenüber eher einseitig zusammengesetzten Güterbündeln, wenn das Gesetz von der abnehmenden Grenzrate der Substitution gilt.
Geht man also davon aus, dass Haushalte eine Präferenz für ausgewogen zusammengesetzte Güterbündel haben, dann gilt das Gesetz von der abnehmenden Grenzrate der Substitution und die Indifferenzkurven haben die typische konvexe Gestalt ( Konvexitätsannahme oder Ausgewogenheitsannahme). Auf einer höheren Aggregationsebene der Güter trifft diese Annahme sicherlich zu. Sei ein Gut "Kleidung" und das andere "Nahrung". Hätten die Haushalte Präferenzen mit einer konstanten Grenzrate der Substitution zwischen diesen beiden Gütern, dann könnte man sie mit genügend Nahrung dazu bewegen, nackt umher zu laufen. Umgekehrt könnte man sie mit genügend Kleidung dazu bewegen, auf's Essen zu verzichten. Es spricht doch einiges dafür, dass die Haushalte eine gesunde Mischung diesen Extremen vorziehen.
Nach ähnlichen Seiten im WWW suchen